Sustitución
El metodo de sustitución consiste en despejar en una de las ecuaciones cualquier incógnita, preferiblemente la que tenga menor coeficiente, para, a continuación, sustituirla en otra ecuación por su valor.
En caso de sistemas con más de dos incógnitas, la seleccionada debe ser sustituida por su valor equivalente en todas las ecuaciones excepto en la que la hemos despejado. En ese instante, tendremos un sistema con una ecuación y una incógnita menos que el inicial, en el que podemos seguir aplicando este método reiteradamente. Por ejemplo, supongamos que queremos resolver por sustitución este sistema:

En la primera ecuación, seleccionamos la incógnita " y" por ser la de menor coeficiente y que posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.
y = 22 - 3X
El siguiente paso será sustituir cada ocurrencia de la incógnita  en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la
en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la  .
.
 en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la
en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la  .
.
Al resolver la ecuación obtenemos el resultado 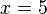 , y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos
, y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos  , con lo que el sistema queda ya resuelto.
, con lo que el sistema queda ya resuelto.
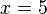 , y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos
, y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos  , con lo que el sistema queda ya resuelto.
, con lo que el sistema queda ya resuelto.Igualación
El método de igualación se puede entender como un caso particular del método de sustitución en el que se despeja la misma incógnita en dos ecuaciones y a continuación se igualan entre sí la parte derecha de ambas ecuaciones.
Tomando el mismo sistema utilizado como ejemplo para el método de sustitución, si despejamos la incógnita  en ambas ecuaciones nos queda de la siguiente manera:
en ambas ecuaciones nos queda de la siguiente manera:
 en ambas ecuaciones nos queda de la siguiente manera:
en ambas ecuaciones nos queda de la siguiente manera:Como se puede observar, ambas ecuaciones comparten la misma parte izquierda, por lo que podemos afirmar que las partes derechas también son iguales entre sí.
Una vez obtenido el valor de la incógnita  , se substituye su valor en una de las ecuaciones originales, y se obtiene obtener el valor de la
, se substituye su valor en una de las ecuaciones originales, y se obtiene obtener el valor de la  .
.
 , se substituye su valor en una de las ecuaciones originales, y se obtiene obtener el valor de la
, se substituye su valor en una de las ecuaciones originales, y se obtiene obtener el valor de la  .
.La forma más fácil de tener el método de sustitución es realizando un cambio para despejar x después de averiguar el valor de la y.
Reducción
Este método suele emplearse mayoritariamente en los sistemas lineales, siendo pocos los casos en que se utiliza para resolver sistemas no lineales. El procedimiento, diseñado para sistemas con dos ecuaciones e incógnitas, consiste en transformar una de las ecuaciones (generalmente, mediante productos), de manera que obtengamos dos ecuaciones en la que una misma incógnita aparezca con el mismo coeficiente y distinto signo. A continuación, se suman ambas ecuaciones produciéndose así la reducción o cancelación de dicha incógnita, obteniendo así una ecuación con una sola incógnita, donde el método de resolución es simple.
Por ejemplo, en el sistema:
no tenemos más que multiplicar la primera ecuación por 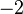 para poder cancelar la incógnita
para poder cancelar la incógnita  . Al multiplicar, dicha ecuación nos queda así:
. Al multiplicar, dicha ecuación nos queda así:
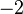 para poder cancelar la incógnita
para poder cancelar la incógnita  . Al multiplicar, dicha ecuación nos queda así:
. Al multiplicar, dicha ecuación nos queda así:Si sumamos esta ecuación a la segunda del sistema original, obtenemos una nueva ecuación donde la incógnita  ha sido reducida y que, en este caso, nos da directamente el valor de la incógnita
ha sido reducida y que, en este caso, nos da directamente el valor de la incógnita  :
:
 ha sido reducida y que, en este caso, nos da directamente el valor de la incógnita
ha sido reducida y que, en este caso, nos da directamente el valor de la incógnita  :
:El siguiente paso consiste únicamente en sustituir el valor de la incógnita  en cualquiera de las ecuaciones donde aparecían ambas incógnitas, y obtener así que el valor de
en cualquiera de las ecuaciones donde aparecían ambas incógnitas, y obtener así que el valor de  es igual a:
es igual a:
 en cualquiera de las ecuaciones donde aparecían ambas incógnitas, y obtener así que el valor de
en cualquiera de las ecuaciones donde aparecían ambas incógnitas, y obtener así que el valor de  es igual a:
es igual a:Regla de Cramer
La regla de Cramer da una solución para sistemas compatibles determinados en términos de determinantes y adjuntos dada por:
Donde Aj es la matriz resultante de remplazar la j-ésima columna de A por el vector columna b. Para un sistema de dos ecuaciones y dos incónitas:
La regla de Cramer da la siguiente solución:
Nota: Cuando en la determinante original det(A) el resultado es 0, el sistema indica múltiples o sin coincidencia.
http://es.wikipedia.org/wiki/Sistema_de_ecuaciones_lineales
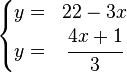


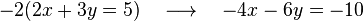







2 comentarios:
hola soy matias ringler de ingles
y tenog que comentar tu blog...xd
bueno me gusta esta interesante aunque no me gusta muhco las matematicas... pero bueno hay que cumplir con el trabajo..espero que estes bien..y con respecto al blogg..e nunca aprendi a hacer un sistema de ecuaciones...xd
Hi Im Margioret, student of English... Its very interesting your blog and funny but I dont like math ....well bye...
Publicar un comentario